7. Model checking and diagnostics¶
7.1. Convergence Diagnostics¶
Valid inferences from sequences of MCMC samples are based on the assumption that the samples are derived from the true posterior distribution of interest. Theory guarantees this condition as the number of iterations approaches infinity. It is important, therefore, to determine the minimum number of samples required to ensure a reasonable approximation to the target posterior density. Unfortunately, no universal threshold exists across all problems, so convergence must be assessed independently each time MCMC estimation is performed. The procedures for verifying convergence are collectively known as convergence diagnostics.
One approach to analyzing convergence is analytical, whereby the variance of the sample at different sections of the chain are compared to that of the limiting distribution. These methods use distance metrics to analyze convergence, or place theoretical bounds on the sample variance, and though they are promising, they are generally difficult to use and are not prominent in the MCMC literature. More common is a statistical approach to assessing convergence. With this approach, rather than considering the properties of the theoretical target distribution, only the statistical properties of the observed chain are analyzed. Reliance on the sample alone restricts such convergence criteria to heuristics. As a result, convergence cannot be guaranteed. Although evidence for lack of convergence using statistical convergence diagnostics will correctly imply lack of convergence in the chain, the absence of such evidence will not guarantee convergence in the chain. Nevertheless, negative results for one or more criteria may provide some measure of assurance to users that their sample will provide valid inferences.
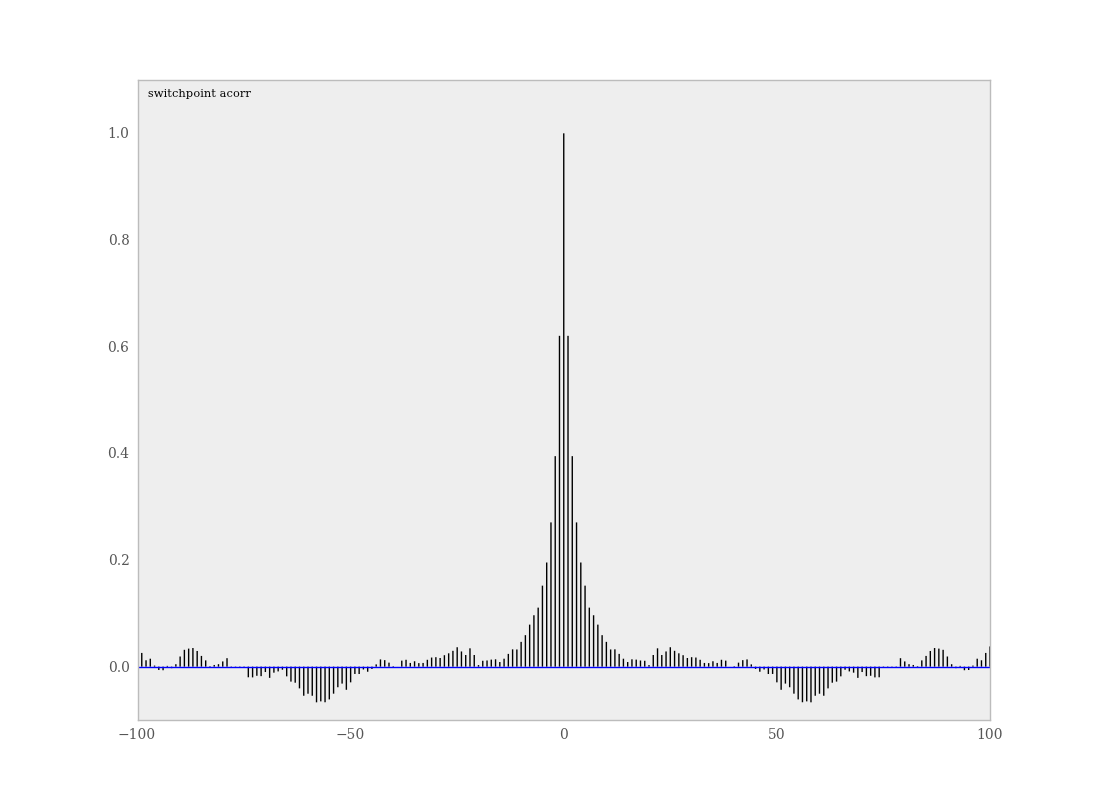
For most simple models, convergence will occur quickly, sometimes within a the first several hundred iterations, after which all remaining samples of the chain may be used to calculate posterior quantities. For more complex models, convergence requires a significantly longer burn-in period; sometimes orders of magnitude more samples are needed. Frequently, lack of convergence will be caused by poor mixing (Figure 7.1). Recall that mixing refers to the degree to which the Markov chain explores the support of the posterior distribution. Poor mixing may stem from inappropriate proposals (if one is using the Metropolis-Hastings sampler) or from attempting to estimate models with highly correlated variables.
An example of a poorly-mixing sample in two dimensions. Notice that the chain is trapped in a region of low probability relative to the mean (dot) and variance (oval) of the true posterior quantity.
7.1.1. Informal Methods¶
The most straightforward approach for assessing convergence is based on simply plotting and inspecting traces and histograms of the observed MCMC sample. If the trace of values for each of the stochastics exhibits asymptotic behavior [1] over the last \(m\) iterations, this may be satisfactory evidence for convergence. A similar approach involves plotting a histogram for every set of \(k\) iterations (perhaps 50-100) beyond some burn in threshold \(n\); if the histograms are not visibly different among the sample intervals, this is reasonable evidence for convergence. Note that such diagnostics should be carried out for each stochastic estimated by the MCMC algorithm, because convergent behavior by one variable does not imply evidence for convergence for other variables in the analysis. An extension of this approach can be taken when multiple parallel chains are run, rather than just a single, long chain. In this case, the final values of \(c\) chains run for \(n\) iterations are plotted in a histogram; just as above, this is repeated every \(k\) iterations thereafter, and the histograms of the endpoints are plotted again and compared to the previous histogram. This is repeated until consecutive histograms are indistinguishable.
Another ad hoc method for detecting lack of convergence is to examine the traces of several MCMC chains initialized with different starting values. Overlaying these traces on the same set of axes should (if convergence has occurred) show each chain tending toward the same equilibrium value, with approximately the same variance. Recall that the tendency for some Markov chains to converge to the true (unknown) value from diverse initial values is called ergodicity. This property is guaranteed by the reversible chains constructed using MCMC, and should be observable using this technique. Again, however, this approach is only a heuristic method, and cannot always detect lack of convergence, even though chains may appear ergodic.
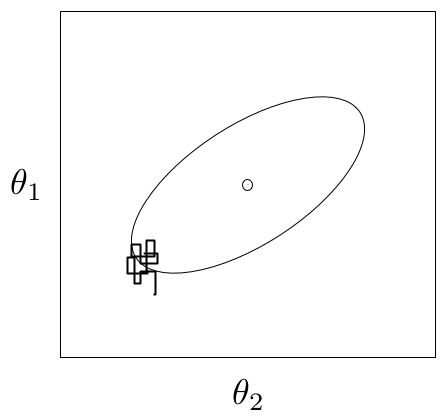
An example of metastability in a two-dimensional parameter space. The chain appears to be stable in one region of the parameter space for an extended period, then unpredictably jumps to another region of the space.
A principal reason that evidence from informal techniques cannot guarantee convergence is a phenomenon called metastability. Chains may appear to have converged to the true equilibrium value, displaying excellent qualities by any of the methods described above. However, after some period of stability around this value, the chain may suddenly move to another region of the parameter space (Figure 7.2). This period of metastability can sometimes be very long, and therefore escape detection by these convergence diagnostics. Unfortunately, there is no statistical technique available for detecting metastability.
7.1.2. Formal Methods¶
Along with the ad hoc techniques described above, a number of more formal methods exist which are prevalent in the literature. These are considered more formal because they are based on existing statistical methods, such as time series analysis.
PyMC currently includes three formal convergence diagnostic methods. The first, proposed by [Geweke1992], is a time-series approach that compares the mean and variance of segments from the beginning and end of a single chain.
where \(a\) is the early interval and \(b\) the late interval. If the z-scores (theoretically distributed as standard normal variates) of these two segments are similar, it can provide evidence for convergence. PyMC calculates z-scores of the difference between various initial segments along the chain, and the last 50% of the remaining chain. If the chain has converged, the majority of points should fall within 2 standard deviations of zero.
Diagnostic z-scores can be obtained by calling the geweke function. It
accepts either (1) a single trace, (2) a Node or Stochastic object, or (4) an
entire Model object:
geweke(x, first=0.1, last=0.5, intervals=20)
The arguments expected are the following:
pymc_object: The object that is or contains the output trace(s).first(optional): First portion of chain to be used in Geweke diagnostic. Defaults to 0.1 (i.e. first 10% of chain).last(optional): Last portion of chain to be used in Geweke diagnostic. Defaults to 0.5 (i.e. last 50% of chain).intervals(optional): Number of sub-chains to analyze. Defaults to 20.
The resulting scores are best interpreted graphically, using the
geweke_plot function. This displays the scores in series, in relation to
the 2 standard deviation boundaries around zero. Hence, it is easy to see
departures from the standard normal assumption.
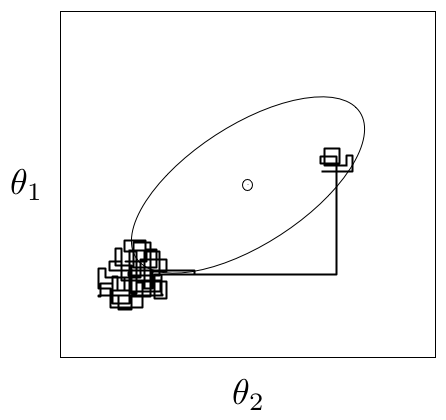
Sample plot of Geweke z-scores for a variable using geweke_plot.
The occurrence of the scores well within 2 standard deviations of zero
gives not indicate of lack of convergence (top), while deviations exceeding
2 standard deviations suggest that additional samples are requred to
achieve convergence (bottom).
geweke_plot takes either a single set of scores, or a dictionary of scores
(output by geweke when an entire Sampler is passed) as its argument:
def geweke_plot(scores, name='geweke', format='png', suffix='-diagnostic',
path='./', fontmap = {1:10, 2:8, 3:6, 4:5, 5:4}, verbose=1)
The arguments are defined as:
scores: The object that contains the Geweke scores. Can be a list (one set) or a dictionary (multiple sets).name(optional): Name used for output files. For multiple scores, the dictionary keys are used as names.format(optional): Graphic output file format (defaults to png).suffix(optional): Suffix to filename (defaults to -diagnostic)path(optional): The path for output graphics (defaults to working directory).fontmap(optional): Dictionary containing the font map for the labels of the graphic.verbose(optional): Verbosity level for output (defaults to 1).
To illustrate, consider the sample model gelman_bioassay that is used to
instantiate a MCMC sampler. The sampler is then run for a given number of
iterations:
>>> from pymc.examples import gelman_bioassay
>>> S = pymc.MCMC(gelman_bioassay)
>>> S.sample(10000, burn=5000)
It is easiest simply to pass the entire sampler S the geweke function:
>>> scores = pymc.geweke(S, intervals=20)
>>> pymc.Matplot.geweke_plot(scores)
Alternatively, individual stochastics within S can be analyzed for
convergence:
>>> trace = S.trace("alpha")[:]
>>> alpha_scores = pymc.geweke(trace, intervals=20)
>>> pymc.Matplot.geweke_plot(alpha_scores, "alpha")
An example of convergence and non-convergence of a chain using geweke_plot is given in Figure 7.3.
The second diagnostic provided by PyMC is the [Raftery1995a] procedure. This approach estimates the number of iterations required to reach convergence, along with the number of burn-in samples to be discarded and the appropriate thinning interval. A separate estimate of both quantities can be obtained for each variable in a given model.
As the criterion for determining convergence, the Raftery and Lewis approach uses the accuracy of estimation of a user-specified quantile. For example, we may want to estimate the quantile \(q=0.975\) to within \(r=0.005\) with probability \(s=0.95\). In other words,
From any sample of \(\theta\), one can construct a binary chain:
where \(u_q\) is the quantile value and \(I\) is the indicator function. While \(\{\theta^{(j)}\}\) is a Markov chain, \(\{Z^{(j)}\}\) is not necessarily so. In any case, the serial dependency among \(Z^{(j)}\) decreases as the thinning interval \(k\) increases. A value of \(k\) is chosen to be the smallest value such that the first order Markov chain is preferable to the second order Markov chain.
This thinned sample is used to determine number of burn-in samples. This is done by comparing the remaining samples from burn-in intervals of increasing length to the limiting distribution of the chain. An appropriate value is one for which the truncated sample’s distribution is within \(\epsilon\) (arbitrarily small) of the limiting distribution. See [Raftery1995a] or [Gamerman1997] for computational details. Estimates for sample size tend to be conservative.
This diagnostic is best used on a short pilot run of a particular model, and the results used to parameterize a subsequent sample that is to be used for inference. Its calling convention is as follows:
raftery_lewis(x, q, r, s=.95, epsilon=.001, verbose=1)
The arguments are:
pymc_object: The object that contains the Geweke scores. Can be a list (one set) or a dictionary (multiple sets).q: Desired quantile to be estimated.r: Desired accuracy for quantile.s(optional): Probability of attaining the requested accuracy (defaults to 0.95).epsilon(optional) : Half width of the tolerance interval required for the q-quantile (defaults to 0.001).verbose(optional) : Verbosity level for output (defaults to 1).
The code for raftery_lewis is based on the FORTRAN program gibbsit
([Raftery1995b]).
For example, consider again a sampler S run for some model my_model:
>>> S = pymc.MCMC(my_model)
>>> S.sample(10000, burn=5000)
One can pass either the entire sampler S or any stochastic within S to the raftery_lewis function, along with suitable arguments. Here, we have chosen \(q = 0.025\) (the lower limit of the equal-tailed 95% interval) and error \(r = 0.01\):
>>> pymc.raftery_lewis(S, q=0.025, r=0.01)
This yields diagnostics as follows for each stochastic of S, as well as a dictionary containing the diagnostic quantities:
========================
Raftery-Lewis Diagnostic
========================
937 iterations required (assuming independence) to achieve 0.01 accuracy
with 95 percent probability.
Thinning factor of 1 required to produce a first-order Markov chain.
39 iterations to be discarded at the beginning of the simulation (burn-in).
11380 subsequent iterations required.
Thinning factor of 11 required to produce an independence chain.
The third convergence diagnostic provided by PyMC is the Gelman-Rubin statistic ([Gelman1992]). This diagnostic uses multiple chains to check for lack of convergence, and is based on the notion that if multiple chains have converged, by definition they should appear very similar to one another; if not, one or more of the chains has failed to converge.
The Gelman-Rubin diagnostic uses an analysis of variance approach to assessing convergence. That is, it calculates both the between-chain variance (B) and within-chain variance (W), and assesses whether they are different enough to worry about convergence. Assuming \(m\) chains, each of length \(n\), quantities are calculated by:
for each scalar estimand \(\theta\). Using these values, an estimate of the marginal posterior variance of \(\theta\) can be calculated:
Assuming \(\theta\) was initialized to arbitrary starting points in each chain, this quantity will overestimate the true marginal posterior variance. At the same time, \(W\) will tend to underestimate the within-chain variance early in the sampling run. However, in the limit as \(n \rightarrow \infty\), both quantities will converge to the true variance of \(\theta\). In light of this, the Gelman-Rubin statistic monitors convergence using the ratio:
This is called the potential scale reduction, since it is an estimate of the potential reduction in the scale of \(\theta\) as the number of simulations tends to infinity. In practice, we look for values of \(\hat{R}\) close to one (say, less than 1.1) to be confident that a particular estimand has converged. In PyMC, the function gelman_rubin will calculate \(\hat{R}\) for each stochastic node in the passed model:
>>> pymc.gelman_rubin(S)
{'alpha': 1.0036389589627821,
'beta': 1.001503957313336,
'theta': [1.0013923468783055,
1.0274479503713816,
0.95365716267969636,
1.00267321019079]}
For the best results, each chain should be initialized to highly dispersed starting values for each stochastic node.
By default, when calling the summary_plot function using nodes with multiple chains, the \(\hat{R}\) values will be plotted alongside the posterior intervals.
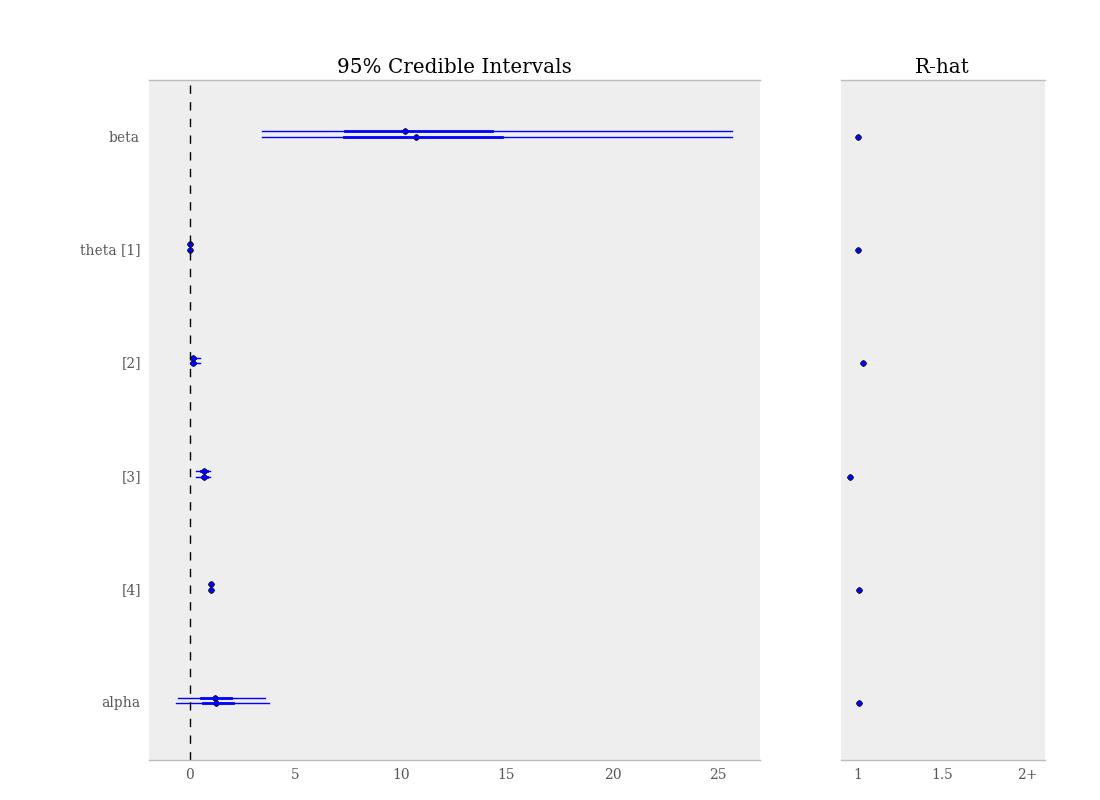
Summary plot of parameters from gelman_bioassay model, showing credible intervals on the left and the Gelman-Rubin statistic on the right.
Additional convergence diagnostics are available in the R statistical
package ([R2010]), via the CODA module ([Plummer2008]). PyMC includes a
method coda for exporting model traces in a format that may be directly
read by coda:
>>> pymc.utils.coda(S)
Generating CODA output
==================================================
Processing deaths
Processing beta
Processing theta
Processing alpha
The lone argument is the PyMC sampler for which output is desired.
Calling coda yields a file containing raw trace values (suffix .out)
and a file containing indices to the trace values (suffix .ind).
7.2. Autocorrelation Plots¶
Samples from MCMC algorithms are ususally autocorrelated, due partly to the inherent Markovian dependence structure. The degree of autocorrelation can be quantified using the autocorrelation function:
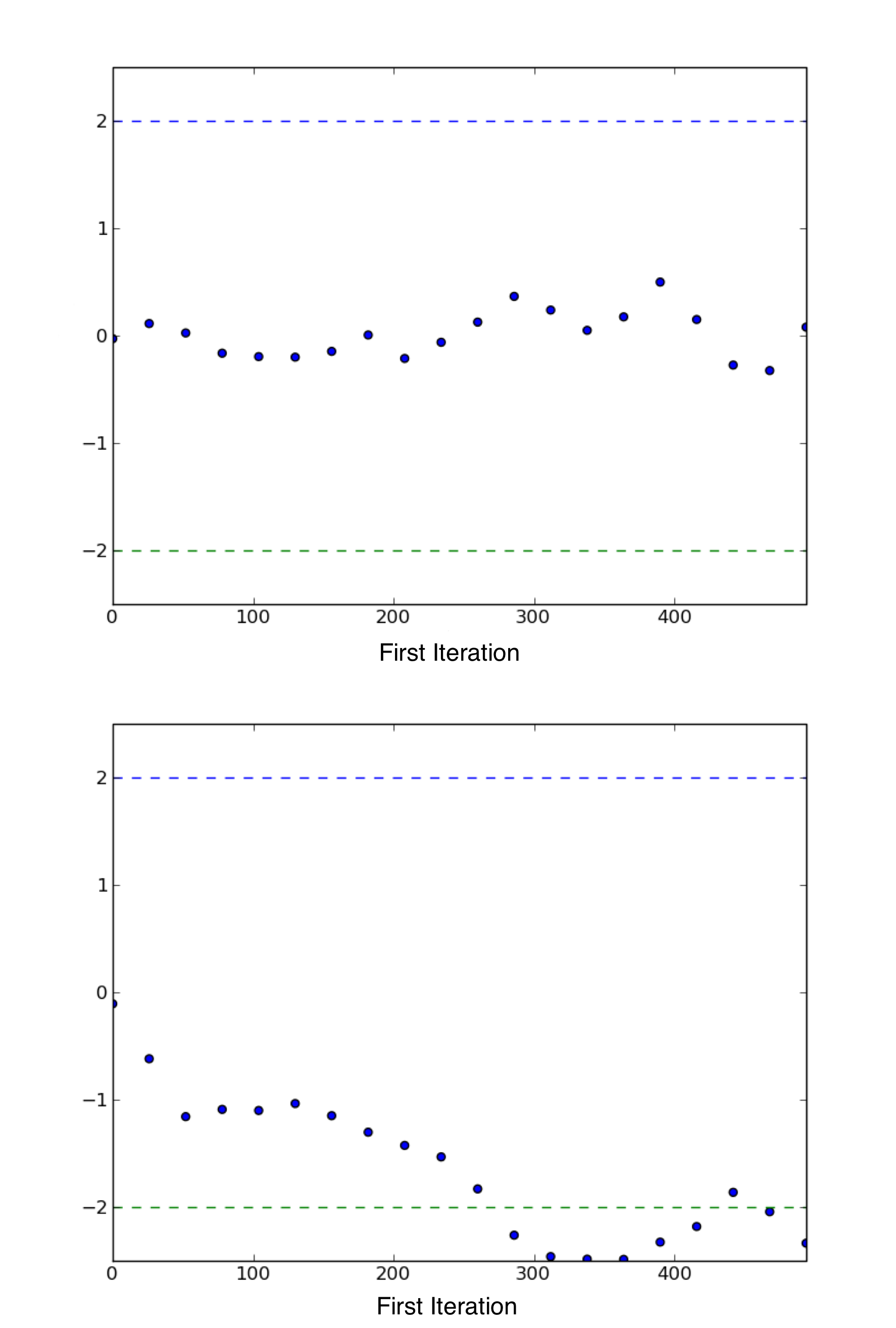
PyMC includes a function for plotting the autocorrelation function for each stochastics in the sampler (Figure 7.5). This allows users to examine the relationship among successive samples within sampled chains. Significant autocorrelation suggests that chains require thinning prior to use of the posterior statistics for inference.
autocorrelation(pymc_object, name, maxlag=100, format='png', suffix='-acf',
path='./', fontmap = {1:10, 2:8, 3:6, 4:5, 5:4}, verbose=1)
pymc_object: The object that is or contains the output trace(s).name: Name used for output files.maxlag: The highest lag interval for which autocorrelation is calculated.format(optional): Graphic output file format (defaults to png).suffix(optional): Suffix to filename (defaults to -diagnostic)path(optional): The path for output graphics (defaults to working directory).fontmap(optional): Dictionary containing the font map for the labels of the graphic.verbose(optional): Verbosity level for output (defaults to 1).
Autocorrelation plots can be obtained simply by passing the sampler to the autocorrelation function (within the Matplot module) directly:
>>> S = pymc.MCMC(gelman_bioassay)
>>> S.sample(10000, burn=5000)
>>> pymc.Matplot.autocorrelation(S)
Alternatively, variables within a model can be plotted individually. For example, the parameter beta that was estimated using sampler S for the gelman_bioassay model will yield a correlation plot as follows:
>>> pymc.Matplot.autocorrelation(S.beta)
7.3. Goodness of Fit¶
Checking for model convergence is only the first step in the evaluation of MCMC model outputs. It is possible for an entirely unsuitable model to converge, so additional steps are needed to ensure that the estimated model adequately fits the data. One intuitive way of evaluating model fit is to compare model predictions with the observations used to fit the model. In other words, the fitted model can be used to simulate data, and the distribution of the simulated data should resemble the distribution of the actual data.
Fortunately, simulating data from the model is a natural component of the Bayesian modelling framework. Recall, from the discussion on imputation of missing data, the posterior predictive distribution:
Here, \(\tilde{y}\) represents some hypothetical new data that would be expected, taking into account the posterior uncertainty in the model parameters. Sampling from the posterior predictive distribution is easy in PyMC. The code looks identical to the corresponding data stochastic, with two modifications: (1) the node should be specified as deterministic and (2) the statistical likelihoods should be replaced by random number generators. As an example, consider a simple dose-response model, where deaths are modeled as a binomial random variable for which the probability of death is a logit-linear function of the dose of a particular drug:
n = [5]*4
dose = [-.86,-.3,-.05,.73]
x = [0,1,3,5]
alpha = pymc.Normal('alpha', mu=0.0, tau=0.01)
beta = pymc.Normal('beta', mu=0.0, tau=0.01)
@pymc.deterministic
def theta(a=alpha, b=beta, d=dose):
"""theta = inv_logit(a+b)"""
return pymc.invlogit(a+b*d)
# deaths ~ binomial(n, p)
deaths = pymc.Binomial('deaths', n=n, p=theta, value=x, observed=True)
The posterior predictive distribution of deaths uses the same functional form as the data likelihood, in this case a binomial stochastic. Here is the corresponding sample from the posterior predictive distribution:
deaths_sim = pymc.Binomial('deaths_sim', n=n, p=theta)
Notice that the observed stochastic pymc.Binomial has been replaced with a stochastic node that is identical in every respect to deaths, except that its values are not fixed to be the observed data – they are left to vary according to the values of the fitted parameters.
The degree to which simulated data correspond to observations can be evaluated in at least two ways. First, these quantities can simply be compared visually. This allows for a qualitative comparison of model-based replicates and observations. If there is poor fit, the true value of the data may appear in the tails of the histogram of replicated data, while a good fit will tend to show the true data in high-probability regions of the posterior predictive distribution (Figure 7.6).
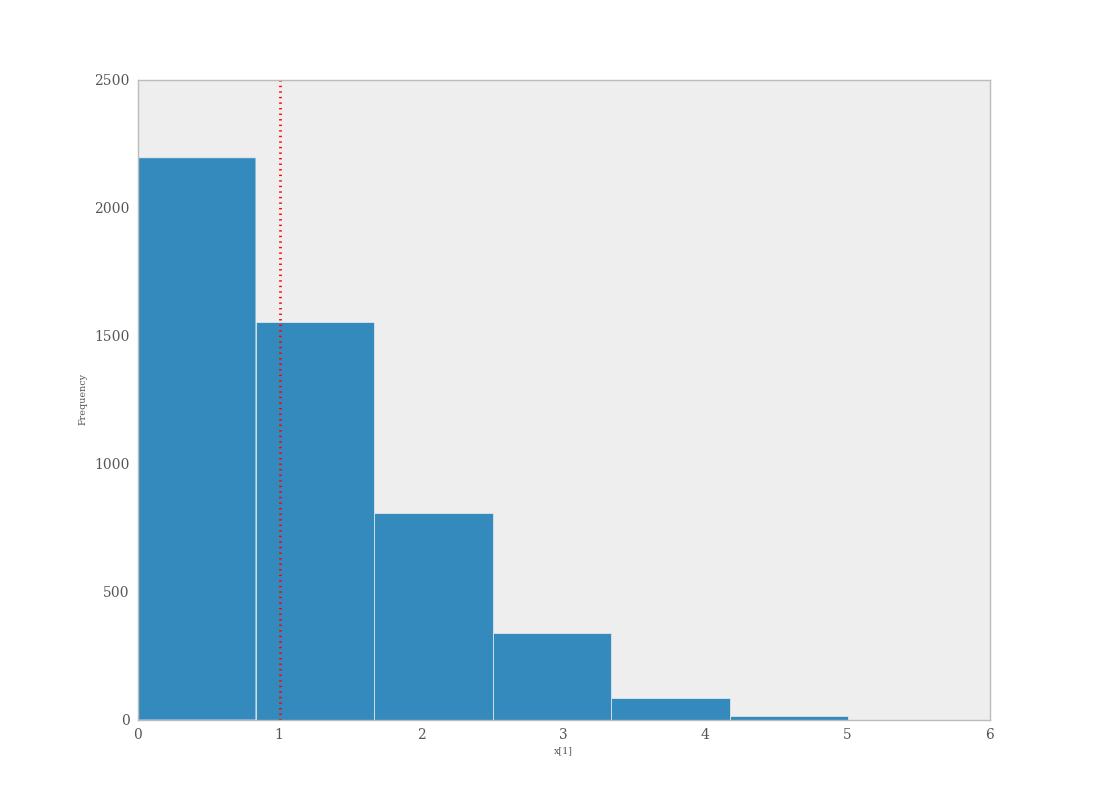
Data sampled from the posterior predictive distribution of a binomial random variate. The observed value (1) is shown by the dotted red line.
The Matplot package in PyMC provides an easy way of producing such plots, via
the gof_plot function. To illustrate, consider a single data point x
and an array of values x_sim sampled from the posterior predictive
distribution. The histogram is generated by calling:
pymc.Matplot.gof_plot(x_sim, x, name='x')
A second approach for evaluating goodness of fit using samples from the posterior predictive distribution involves the use of a statistical criterion. For example, the Bayesian p-value [Gelman1996] uses a discrepancy measure that quantifies the difference between data (observed or simulated) and the expected value, conditional on some model. One such discrepancy measure is the Freeman-Tukey statistic [Brooks2000]:
where the \(x_j\) are data and \(e_j\) are the corresponding expected values, based on the model. Model fit is assessed by comparing the discrepancies from observed data to those from simulated data. On average, we expect the difference between them to be zero; hence, the Bayesian p value is simply the proportion of simulated discrepancies that are larger than their corresponding observed discrepancies:
If \(p\) is very large (e.g. \(>0.975\)) or very small (e.g. \(<0.025\)) this implies that the model is not consistent with the data, and thus is evidence of lack of fit. Graphically, data and simulated discrepancies plotted together should be clustered along a 45 degree line passing through the origin, as shown in Figure 7.7.
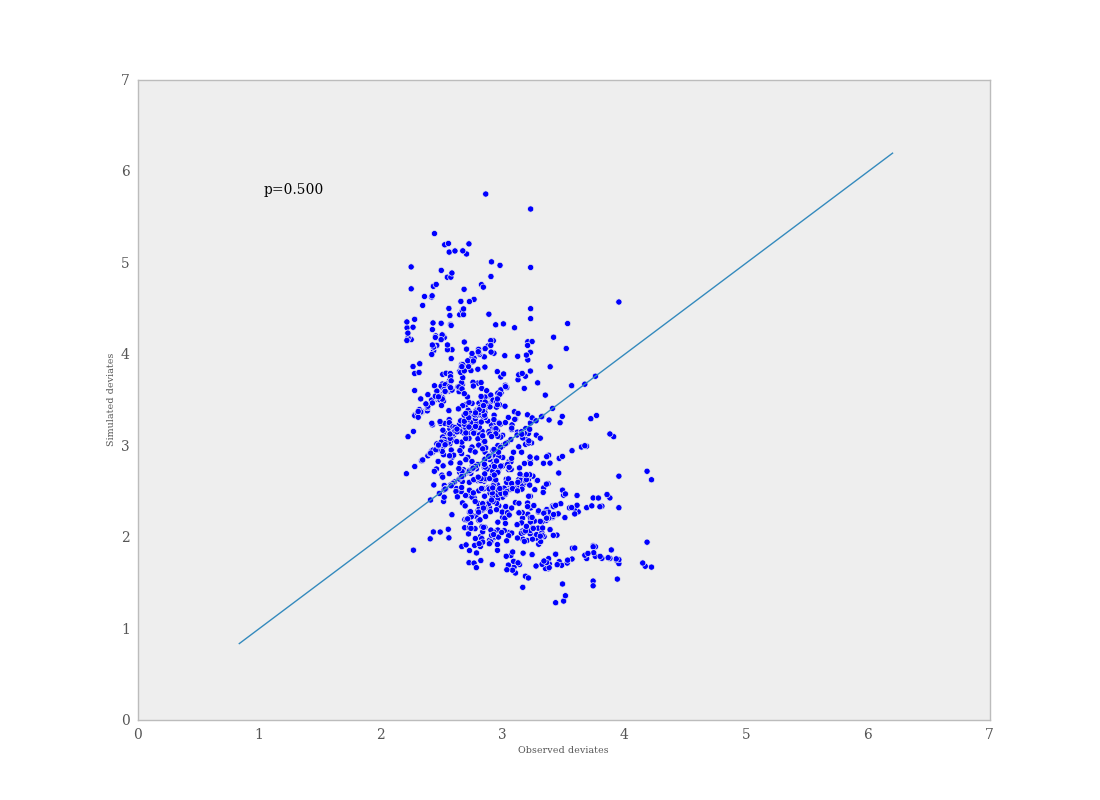
Plot of deviates of observed and simulated data from expected values. The cluster of points symmetrically about the 45 degree line (and the reported p-value) suggests acceptable fit for the modeled parameter.
The discrepancy function in the diagnostics package can be used to
generate discrepancy statistics from arrays of data, simulated values, and
expected values:
D = pymc.discrepancy(x, x_sim, x_exp)
For a dataset of size \(n\) and an MCMC chain of length \(r\), this
implies that x is size (n,), x_sim is size (r,n) and x_exp
is either size (r,) or (r,n). A call to this function returns two
arrays of discrepancy values (simulated and observed), which can be passed to
the discrepancy_plot function in the Matplot module to generate a scatter
plot, and if desired, a p value:
pymc.Matplot.discrepancy_plot(D, name='D', report_p=True)
Additional optional arguments for discrepancy_plot are identical to other
PyMC plotting functions.
Footnotes
| [1] | Asymptotic behaviour implies that the variance and the mean value of the sample stays relatively constant over some arbitrary period. |